None

Note

This tutorial was generated from an IPython notebook that can be accessed from github.

Create 3D mask of approximate fractional overlap

Working with fractional overlap - indicating how much of the grid cell is covered by the region - can help to create more exact regional means, allow to exclude gridpoints from regions if the overlap is too small etc.. Since v0.12.0 regionmask can create a 3D masks with the approximate fractional overlap of a set of regions for equally-spaced latitude and longitude grids. The mask is a float xarray.DataArray with shape region x lat x lon, with the overlap given as fraction (i.e. between 0 and 1).

Attention

There are three caveats when creating fractional overlaps:

1. The passed longitude and latitude coordinates must be equally spaced - otherwise an InvalidCoordsError is raised.

2. Calculating the fractional overlap can be memory intensive (especially when passing many coordinates).

3. The resulting mask is correct to about 0.05 (i.e. 5%).

Despite these restrictions using an approximation has advantages over calculating the exact overlap - it is considerably faster. Many concepts were already introduced in 3D masks.

Import libraries and check the regionmask version:

import numpy as np
import xarray as xr

import regionmask

# don't expand data
xr.set_options(display_style="text", display_expand_data=False, display_width=60)

regionmask.__version__

'0.12.1'

Creating a mask

Define a lon/ lat grid with a 2° grid spacing, where the points define the center of the grid:

lon = np.arange(0, 360, 2)
lat = np.arange(90, -91, -2)

The function mask_3D_frac_approx calculates the fractional overlap of each gridpoint with each region. Here using the AR6 land regions (Iturbide et al., 2020):

mask = regionmask.defined_regions.ar6.land.mask_3D_frac_approx(lon, lat)

Downloading file 'IPCC-WGI-reference-regions-v4.zip' from 'https://github.com/regionmask/regionmask/raw/v0.12.1/data/IPCC-WGI-reference-regions-v4.zip' to '/home/docs/.cache/regionmask/v0.12.1'.

Illustration

As mentioned, mask is a float xarray.DataArray with shape region x lat x lon. It contains region (=numbers) as dimension coordinate as well as abbrevs and names as non-dimension coordinates (see the xarray docs for the details on the terminology).

The regions northwestern North-America, and northeastern North-America (regions 1, and 2) look as follows:

import cartopy.crs as ccrs

fg = mask.sel(region=slice(1, 2)).plot(
    subplot_kws=dict(projection=ccrs.PlateCarree()),
    col="region",
    col_wrap=2,
    transform=ccrs.PlateCarree(),
    add_colorbar=True,
    aspect=1.5,
    cmap="Blues",
    cbar_kwargs={"pad": 0.01, "shrink": 0.65},

)

fg.cbar.set_label("Fractional overlap")

for ax in fg.axs.flatten():
    regionmask.defined_regions.ar6.land.plot(ax=ax, add_label=False, line_kws={"lw": 0.5})
    ax.set_extent([-172, -47.5, 35, 90], ccrs.PlateCarree())

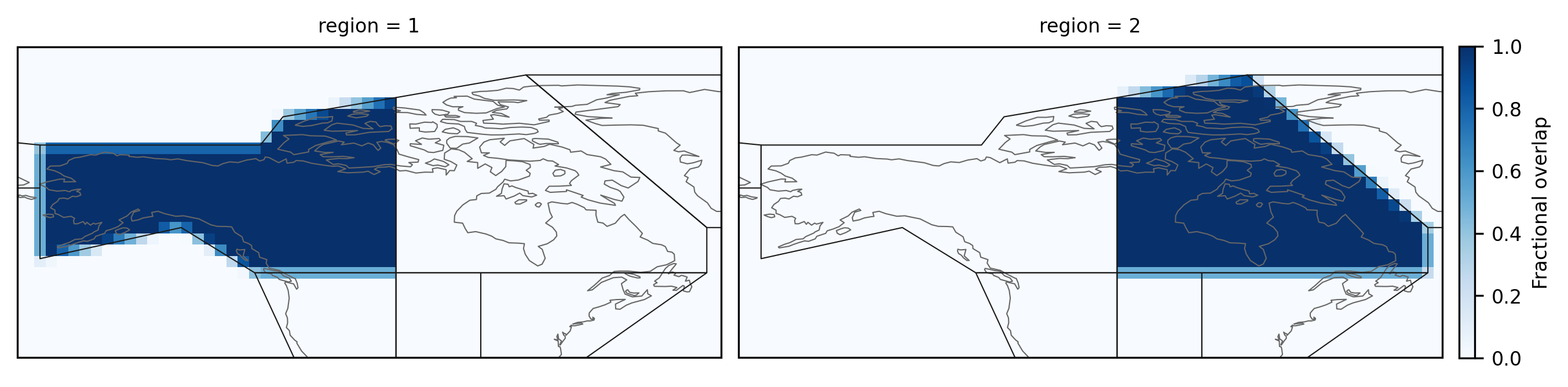
Working with a 3D mask

masks can be used to select data in a certain region and to calculate regional averages. Let’s illustrate this with a ‘real’ dataset - the example data is a temperature field over North America.

airtemps = xr.tutorial.load_dataset("air_temperature")

An xarray object can be passed to the mask_3D_frac_approx function:

mask_3D_frac_approx = regionmask.defined_regions.ar6.land.mask_3D_frac_approx(airtemps)

As airtemps has another grid than the example above, the resulting mask looks different:

fg = mask_3D_frac_approx.sel(region=slice(1, 2)).plot(
    subplot_kws=dict(projection=ccrs.PlateCarree()),
    col="region",
    col_wrap=2,
    transform=ccrs.PlateCarree(),
    add_colorbar=True,
    aspect=1.5,
    cmap="Blues",
    cbar_kwargs={"pad": 0.01, "shrink": 0.65},

)

fg.cbar.set_label("Fractional overlap")

for ax in fg.axs.flatten():
    regionmask.defined_regions.ar6.land.plot(ax=ax, add_label=False, line_kws={"lw": 0.5})
    ax.set_extent([-172, -47.5, 35, 90], ccrs.PlateCarree())

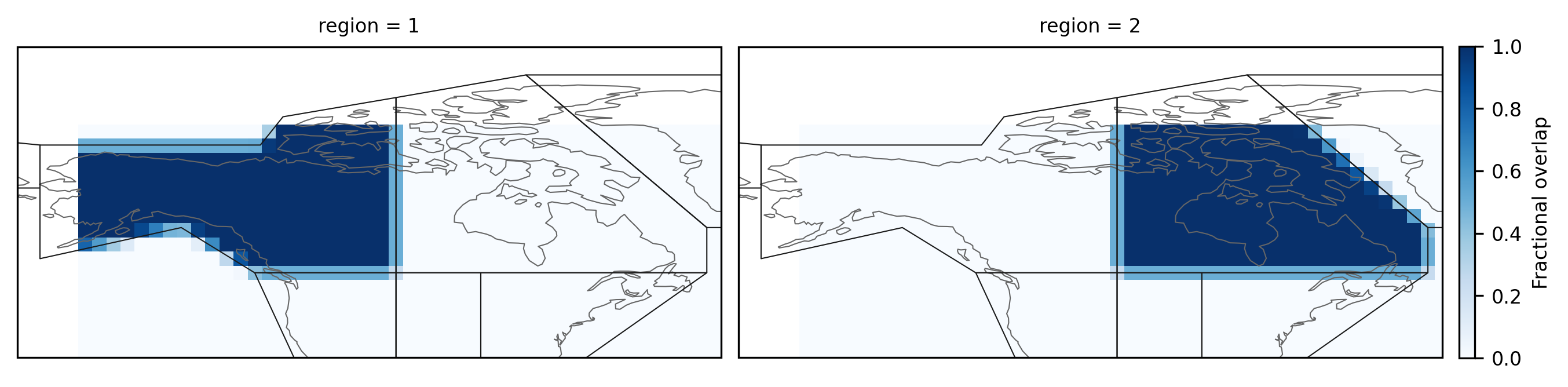
Use an overlap threshold

To restrict the region to gridcells that overlap more to a certain threshold, grid points can be masked out using where:

threshold = 0.5

mask_3D_ge050 = mask_3D_frac_approx.where(mask_3D_frac_approx >= threshold, 0)

This sets all grid points with an overlap of less than 50% to 0. The second options is to convert the fractional mask to a boolean one:

mask_3D_bool = mask_3D_frac_approx >= threshold

Calculate weighted regional averages

As for the boolan 3D mask, we can calculate the regional averages using fractional mask. In this case each grid point contributes according to its overlap and area. As proxy of the grid cell area we use cos(lat).

Note

It is better to use a model’s original grid cell area (e.g. areacella). cos(lat) works reasonably well for regular lat/ lon grids. For irregular grids (regional models, ocean models, …) it is not appropriate.

weights = np.cos(np.deg2rad(airtemps.lat))

ts_airtemps_regional = airtemps.weighted(mask_3D_frac_approx * weights).mean(dim=("lat", "lon"))

This is almost the same as for the boolean 3D mask: by multiplying mask_3D * weights we get a DataArray where the fractional overlap is scaled by the grid cell area. airtemps.weighted(mask_3D * weights).mean(["lat", "lon"]) calculates the weighted mean over the lat and lon dimensions:

ts_airtemps_regional

<xarray.Dataset> Size: 234kB
Dimensions:  (time: 2920, region: 9)
Coordinates:
  * time     (time) datetime64[ns] 23kB 2013-01-01 ... 20...
  * region   (region) int64 72B 0 1 2 3 4 5 6 7 8
    abbrevs  (region) <U3 108B 'GIC' 'NWN' ... 'SCA' 'CAR'
    names    (region) <U17 612B 'Greenland/Iceland' ... '...
Data variables:
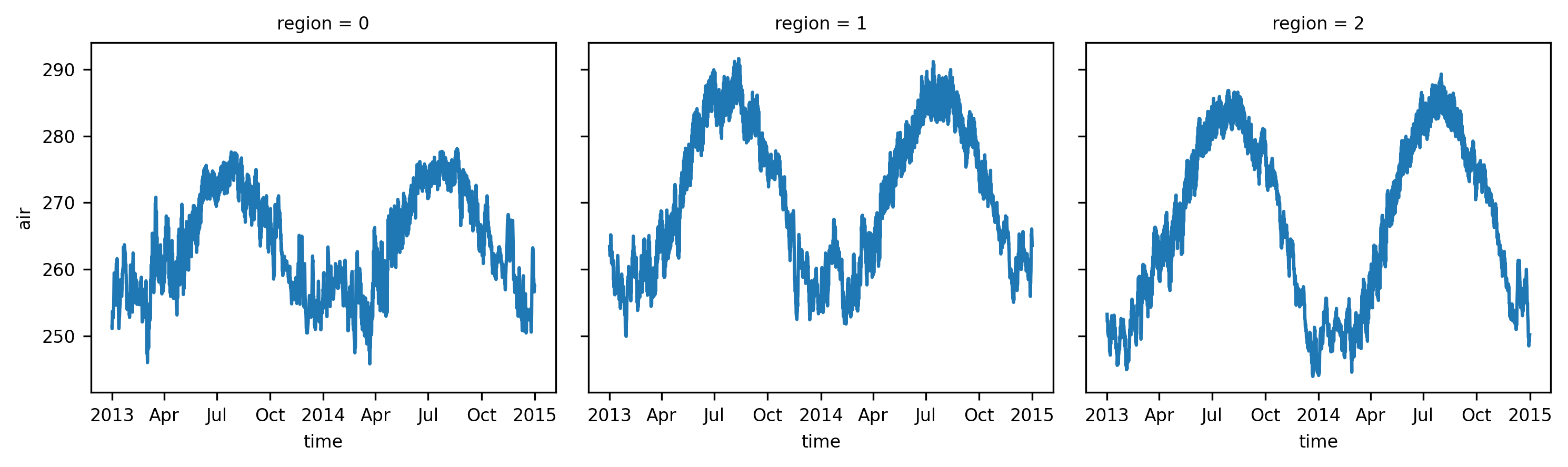
    air      (time, region) float64 210kB 251.4 ... 299.3

The regionally-averaged time series can be plotted:

ts_airtemps_regional.air.sel(region=slice(0, 2)).plot(col="region", col_wrap=3);

References

• Iturbide, M., Gutiérrez, J. M., Alves, L. M., Bedia, J., Cerezo-Mota, R., Cimadevilla, E., Cofiño, A. S., Di Luca, A., Faria, S. H., Gorodetskaya, I. V., Hauser, M., Herrera, S., Hennessy, K., Hewitt, H. T., Jones, R. G., Krakovska, S., Manzanas, R., Martínez-Castro, D., Narisma, G. T., Nurhati, I. S., Pinto, I., Seneviratne, S. I., van den Hurk, B., and Vera, C. S.: An update of IPCC climate reference regions for subcontinental analysis of climate model data: definition and aggregated datasets, Earth Syst. Sci. Data, 12, 2959–2970, https://doi.org/10.5194/essd-12-2959-2020, 2020.