Show code cell content Hide code cell content

%matplotlib inline

from matplotlib import rcParams

rcParams["figure.dpi"] = 300
rcParams["font.size"] = 8

import warnings

warnings.filterwarnings("ignore")

Note

This page was generated from an Jupyter notebook that can be accessed from github.

Create 3D boolean masks

In this tutorial we will show how to create 3D boolean masks for arbitrary latitude and longitude grids. It uses the same algorithm to determine if a gridpoint is in a region as for the 2D mask. However, it returns a xarray.Dataset with shape region x lat x lon, gridpoints that do not fall in a region are False, the gridpoints that fall in a region are True.

3D masks are convenient as they can be used to directly calculate weighted regional means (over all regions) using xarray v0.15.1 or later. Further, the mask includes the region names and abbreviations as non-dimension coordinates.

Tip

3D boolean masks are more convenient to work with but 2D masks may offer some speed gains when calculating regional means. See 226 how weighted regional averages can be calculated with 2D integer mask.

Import regionmask and check the version:

import regionmask

regionmask.__version__

'0.13.0'

Load xarray and numpy:

import numpy as np
import xarray as xr

# don't expand data
xr.set_options(display_style="text", display_expand_data=False, display_width=60)

<xarray.core.options.set_options at 0x7fcc6db82db0>

Creating a mask

Define a lon/ lat grid with a 1° grid spacing, where the points define the center of the grid:

lon = np.arange(-179.5, 180)
lat = np.arange(-89.5, 90)

We will create a mask with the SREX regions (Seneviratne et al., 2012).

regionmask.defined_regions.srex

<regionmask.Regions 'SREX'>
Source:   Seneviratne et al., 2012 (https://www.ipcc.ch/site/assets/uploads/2...
overlap:  False

Regions:
 1 ALA       Alaska/N.W. Canada
 2 CGI     Canada/Greenl./Icel.
 3 WNA         W. North America
 4 CNA         C. North America
 5 ENA         E. North America
..  ..                      ...
22 EAS                  E. Asia
23 SAS                  S. Asia
24 SEA                S.E. Asia
25 NAU             N. Australia
26 SAU S. Australia/New Zealand

[26 regions]

The function mask_3D determines which gripoints lie within the polygon making up each region:

mask = regionmask.defined_regions.srex.mask_3D(lon, lat)
mask

<xarray.DataArray 'mask' (region: 26, lat: 180, lon: 360)> Size: 2MB
False False False False False ... False False False False
Coordinates:
  * lat      (lat) float64 1kB -89.5 -88.5 ... 88.5 89.5
  * lon      (lon) float64 3kB -179.5 -178.5 ... 178.5 179.5
  * region   (region) int64 208B 1 2 3 4 5 ... 23 24 25 26
    abbrevs  (region) <U3 312B 'ALA' 'CGI' ... 'NAU' 'SAU'
    names    (region) <U24 2kB 'Alaska/N.W. Canada' ... '...
Attributes:
    standard_name:  region

As mentioned, mask is a boolean xarray.Dataset with shape region x lat x lon. It contains region (=numbers) as dimension coordinate as well as abbrevs and names as non-dimension coordinates (see the xarray docs for the details on the terminology).

Plotting

Plotting individual layers

The four first layers look as follows:

import cartopy.crs as ccrs
import matplotlib.pyplot as plt
from matplotlib import colors as mplc

cmap1 = mplc.ListedColormap(["none", "#9ecae1"])

fg = mask.isel(region=slice(4)).plot(
    subplot_kws=dict(projection=ccrs.PlateCarree()),
    col="region",
    col_wrap=2,
    transform=ccrs.PlateCarree(),
    add_colorbar=False,
    aspect=1.5,
    cmap=cmap1,
)

for ax in fg.axes.flatten():
    ax.coastlines()

fg.fig.subplots_adjust(hspace=0, wspace=0.1);

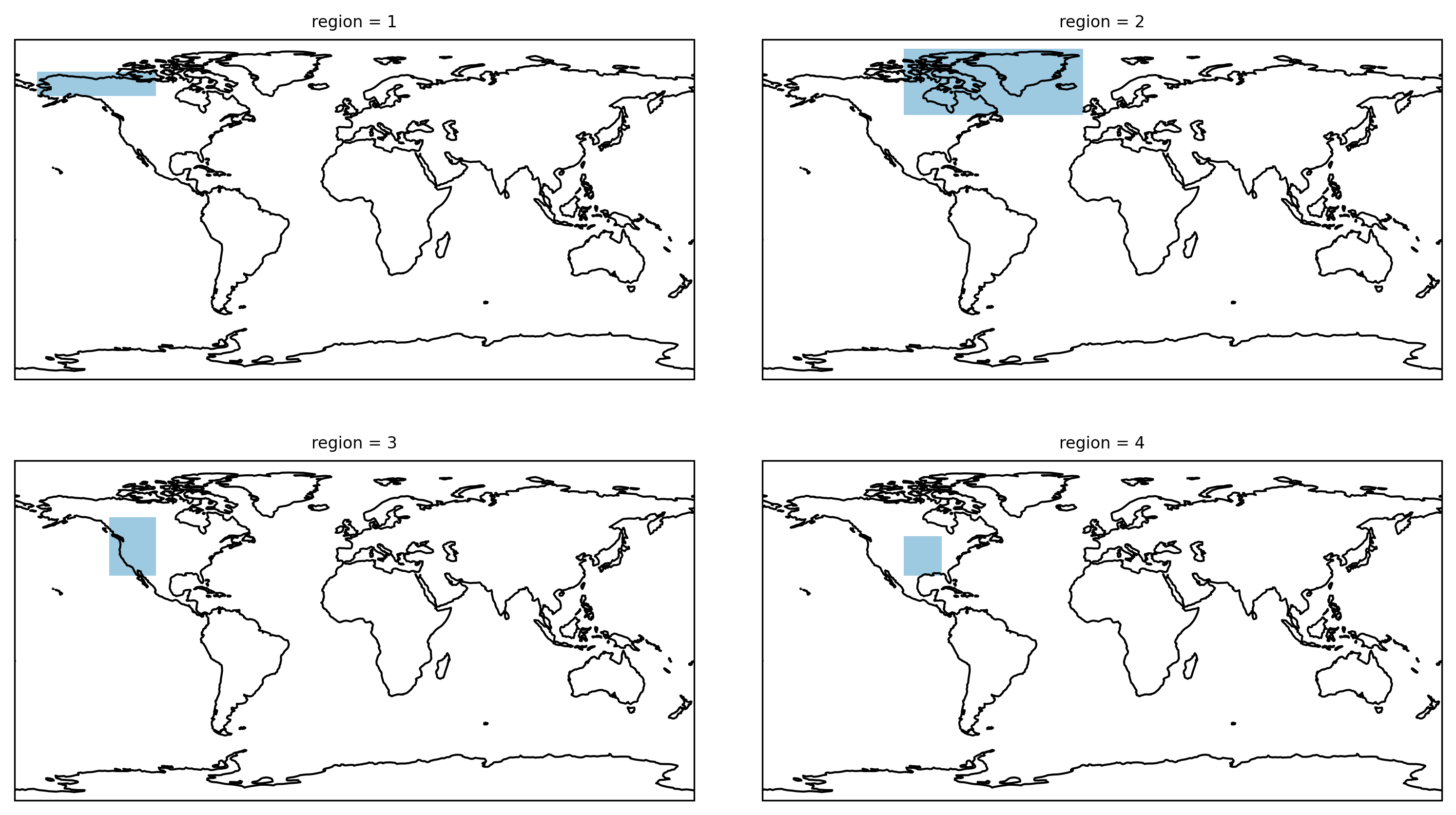
Plotting flattened masks

A 3D mask cannot be directly plotted - it needs to be flattened first. To do this regionmask offers a convenience function: regionmask.plot_3D_mask. The function takes a 3D mask as argument, all other keyword arguments are passed through to xr.plot.pcolormesh.

regionmask.plot_3D_mask(mask, add_colorbar=False, cmap="plasma");

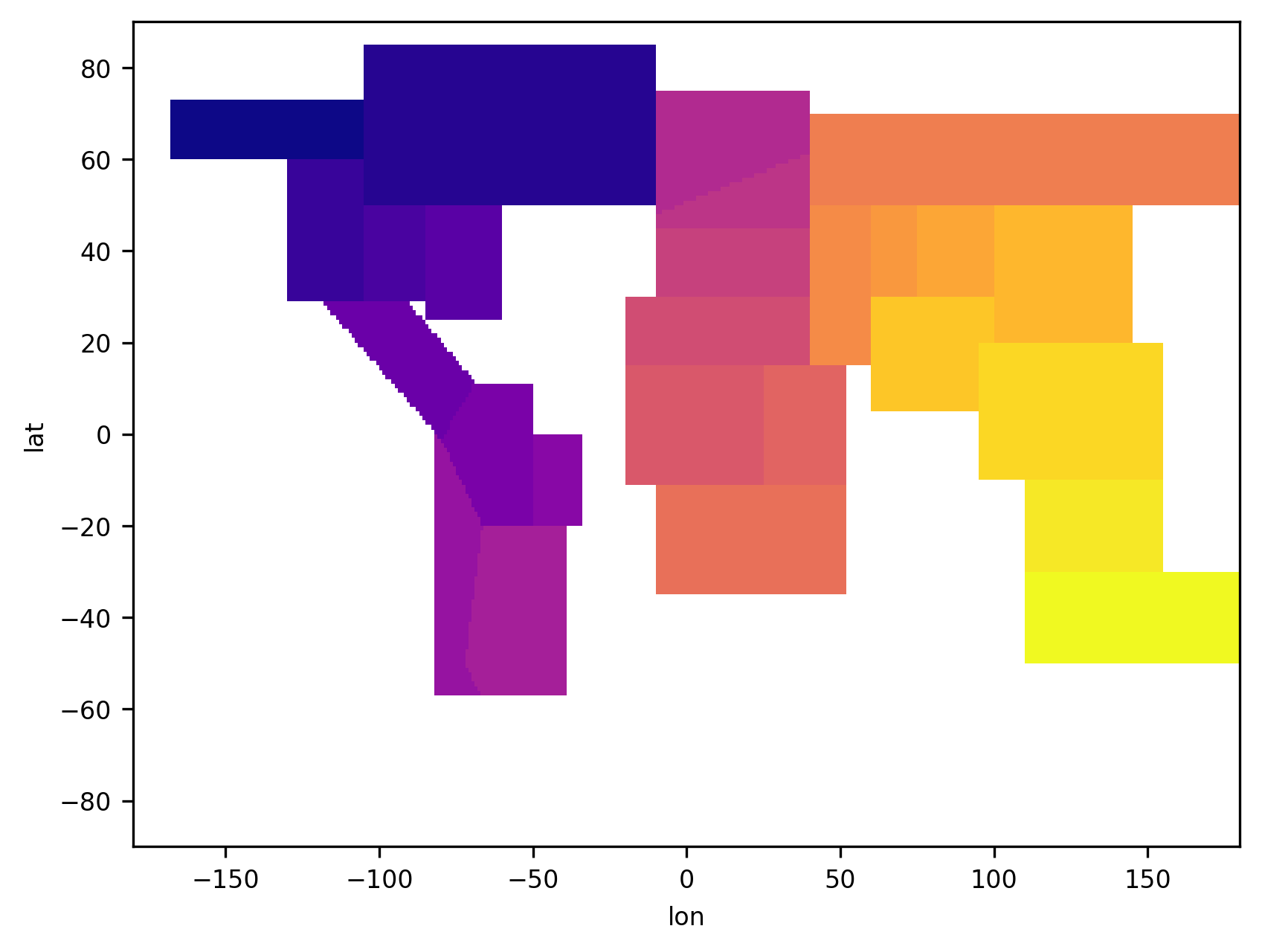
Working with a 3D mask

masks can be used to select data in a certain region and to calculate regional averages - let’s illustrate this with a ‘real’ dataset:

airtemps = xr.tutorial.load_dataset("air_temperature")

The example data is a temperature field over North America. Let’s plot the first time step:

# choose a good projection for regional maps
proj = ccrs.LambertConformal(central_longitude=-100)

ax = plt.subplot(111, projection=proj)

airtemps.isel(time=1).air.plot.pcolormesh(ax=ax, transform=ccrs.PlateCarree())

ax.coastlines()
None

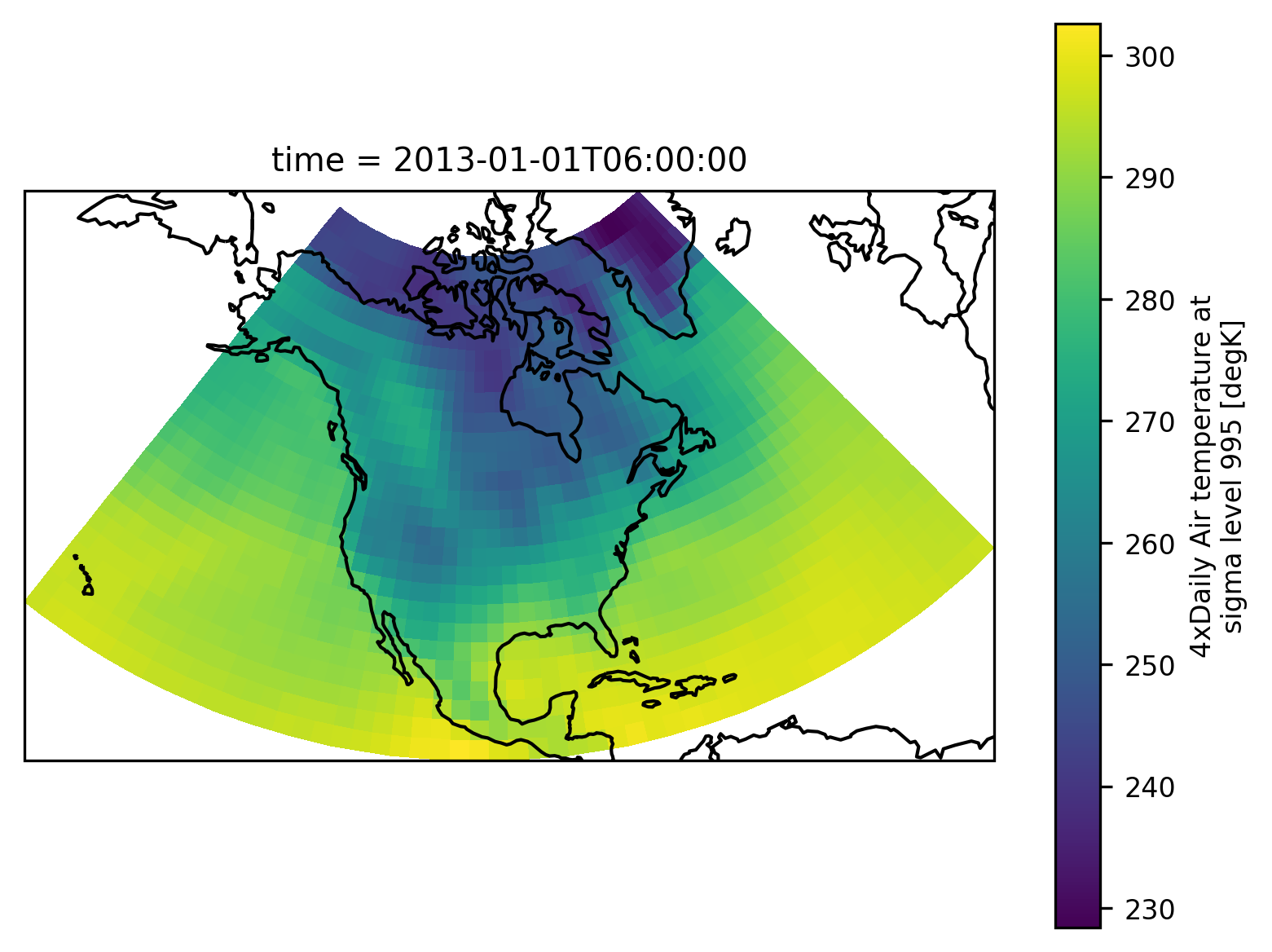
An xarray object can be passed to the mask_3D function:

mask_3D = regionmask.defined_regions.srex.mask_3D(airtemps)
mask_3D

<xarray.DataArray 'mask' (region: 6, lat: 25, lon: 53)> Size: 8kB
False False False False False ... False False False False
Coordinates:
  * lat      (lat) float32 100B 75.0 72.5 70.0 ... 17.5 15.0
  * lon      (lon) float32 212B 200.0 202.5 ... 327.5 330.0
  * region   (region) int64 48B 1 2 3 4 5 6
    abbrevs  (region) <U3 72B 'ALA' 'CGI' ... 'ENA' 'CAM'
    names    (region) <U22 528B 'Alaska/N.W. Canada' ... ...
Attributes:
    standard_name:  region

Per default this creates a mask containing one layer (slice) for each region containing (at least) one gridpoint. As the example data only has values over Northern America we only get only 6 layers even though there are 26 SREX regions. To obtain all layers specify drop=False:

mask_full = regionmask.defined_regions.srex.mask_3D(airtemps, drop=False)
mask_full

<xarray.DataArray 'mask' (region: 26, lat: 25, lon: 53)> Size: 34kB
False False False False False ... False False False False
Coordinates:
  * lat      (lat) float32 100B 75.0 72.5 70.0 ... 17.5 15.0
  * lon      (lon) float32 212B 200.0 202.5 ... 327.5 330.0
  * region   (region) int64 208B 1 2 3 4 5 ... 23 24 25 26
    abbrevs  (region) <U3 312B 'ALA' 'CGI' ... 'NAU' 'SAU'
    names    (region) <U24 2kB 'Alaska/N.W. Canada' ... '...
Attributes:
    standard_name:  region

Note mask_full now has 26 layers.

Select a region

As mask_3D contains region, abbrevs, and names as (non-dimension) coordinates we can use each of those to select an individual region:

# 1) by the index of the region:
r1 = mask_3D.sel(region=3)

# 2) with the abbreviation
r2 = mask_3D.isel(region=(mask_3D.abbrevs == "WNA"))

# 3) with the long name:
r3 = mask_3D.isel(region=(mask_3D.names == "E. North America"))

This also applies to the regionally-averaged data below.

It is currently not possible to use sel with a non-dimension coordinate - to directly select abbrev or name you need to create a MultiIndex:

mask_3D.set_index(regions=["region", "abbrevs", "names"]);

Mask out a region

Using where a specific region can be ‘masked out’ (i.e. all data points outside of the region become NaN):

airtemps_cna = airtemps.where(r1)

Which looks as follows:

proj = ccrs.LambertConformal(central_longitude=-100)

ax = plt.subplot(111, projection=proj)

airtemps_cna.isel(time=1).air.plot(ax=ax, transform=ccrs.PlateCarree())

ax.coastlines()
None

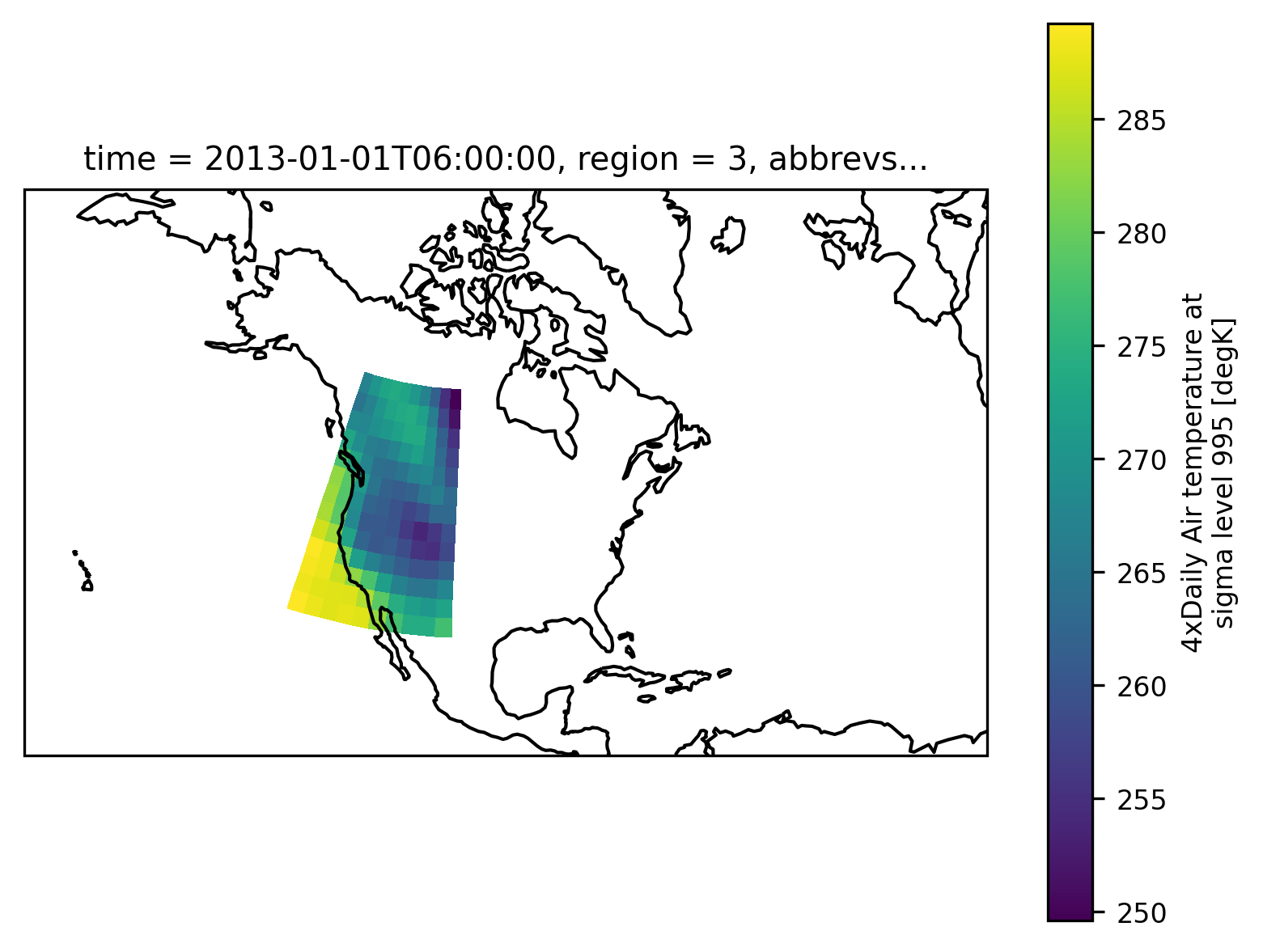
We could now use airtemps_cna to calculate the regional average for ‘Central North America’. However, there is a more elegant way.

Calculate weighted regional averages

Using the 3-dimensional mask it is possible to calculate weighted averages of all regions in one go, using the weighted method (requires xarray 0.15.1 or later). As proxy of the grid cell area we use cos(lat).

Note

It is better to use a model’s original grid cell area (e.g. areacella). cos(lat) works reasonably well for regular lat/ lon grids. For irregular grids (regional models, ocean models, …) it is not appropriate.

weights = np.cos(np.deg2rad(airtemps.lat))

ts_airtemps_regional = airtemps.weighted(mask_3D * weights).mean(dim=("lat", "lon"))

Let’s break down what happens here. By multiplying mask_3D * weights we get a DataArray where gridpoints not in the region get a weight of 0. Gridpoints within a region get a weight proportional to the gridcell area. airtemps.weighted(mask_3D * weights) creates an xarray object which can be used for weighted operations. From this we calculate the weighted mean over the lat and lon dimensions. The resulting dataarray has the dimensions region x time:

ts_airtemps_regional

<xarray.Dataset> Size: 164kB
Dimensions:  (time: 2920, region: 6)
Coordinates:
  * time     (time) datetime64[ns] 23kB 2013-01-01 ... 20...
  * region   (region) int64 48B 1 2 3 4 5 6
    abbrevs  (region) <U3 72B 'ALA' 'CGI' ... 'ENA' 'CAM'
    names    (region) <U22 528B 'Alaska/N.W. Canada' ... ...
Data variables:
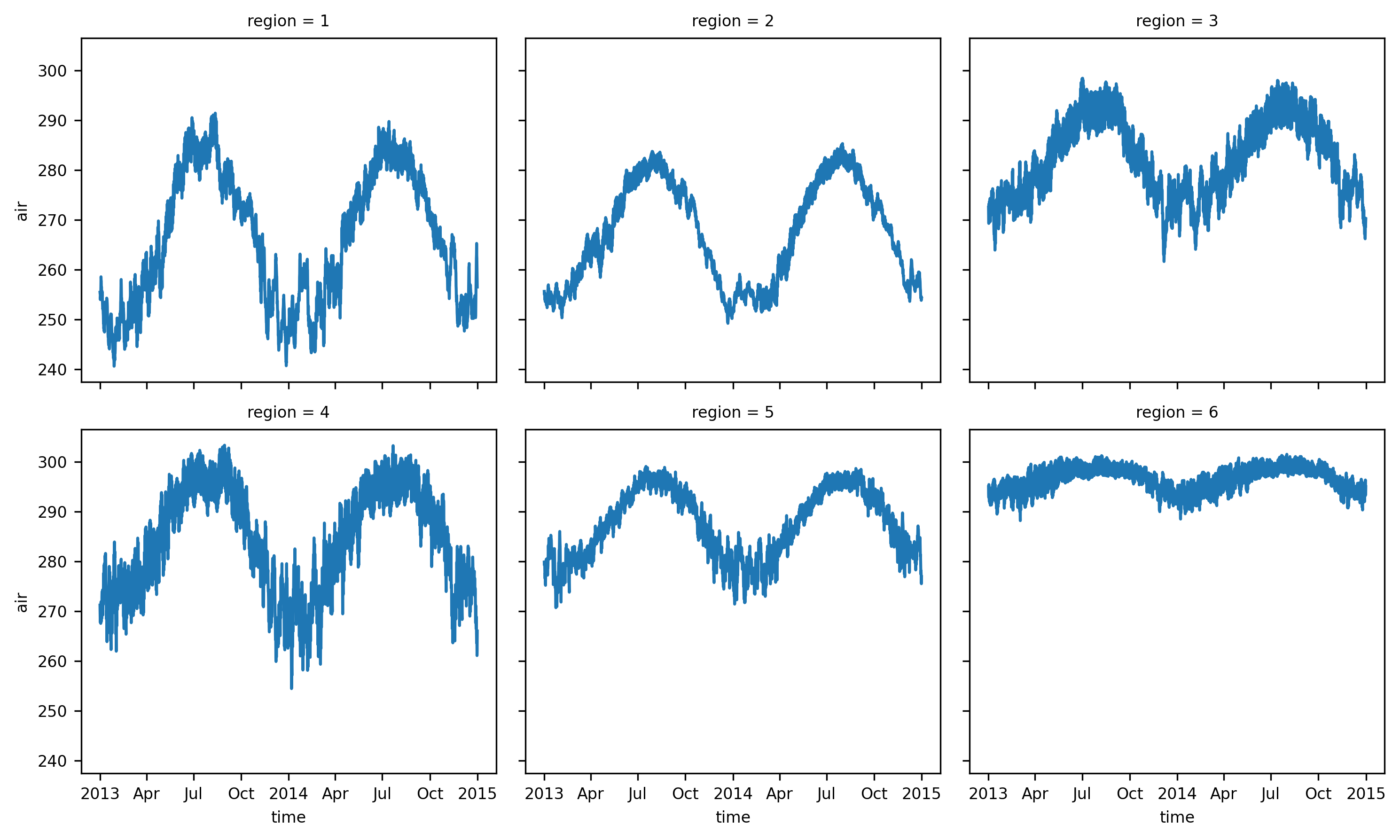
    air      (time, region) float64 140kB 255.5 ... 295.0

The regionally-averaged time series can be plotted:

ts_airtemps_regional.air.plot(col="region", col_wrap=3);

Restrict the mask to land points

Combining the mask of the regions with a land-sea mask we can create a land-only mask using the land_110 region from NaturalEarth.

Warning

It is better to use a model’s original land/ sea mask (e.g. sftlf). Many CMIP models treat the Antarctic ice shelves and the Caspian Sea as land, while it is classified as ‘water’ in natural_earth_v5_0_0.land_110.

With this caveat in mind we can create the land-sea mask:

land_110 = regionmask.defined_regions.natural_earth_v5_0_0.land_110

land_mask = land_110.mask_3D(airtemps)

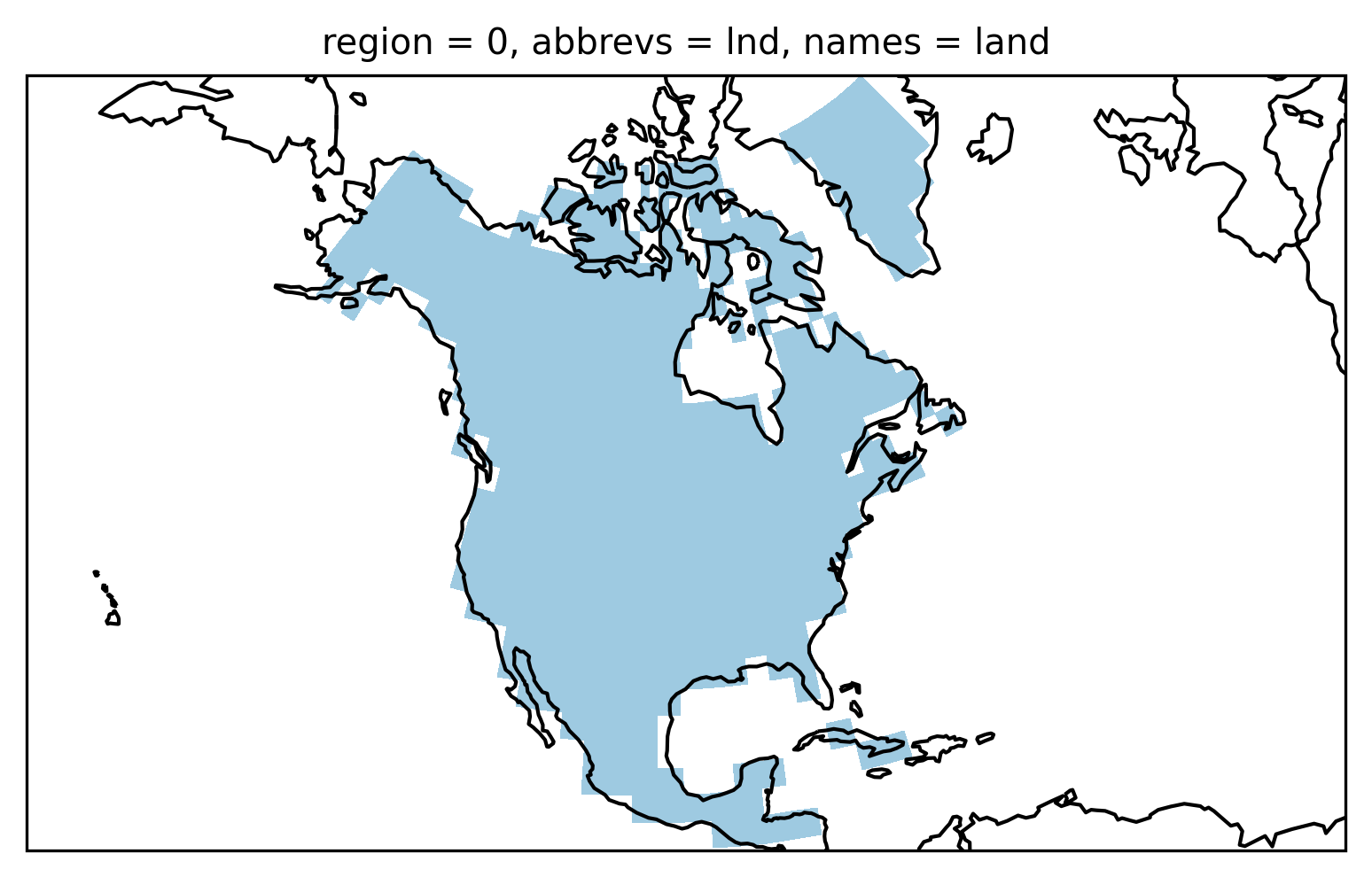
and plot it

proj = ccrs.LambertConformal(central_longitude=-100)

ax = plt.subplot(111, projection=proj)

land_mask.squeeze().plot.pcolormesh(
    ax=ax, transform=ccrs.PlateCarree(), cmap=cmap1, add_colorbar=False
)

ax.coastlines();

To create the combined mask we multiply the two:

mask_lsm = mask_3D * land_mask.squeeze(drop=True)

Note the .squeeze(drop=True). This is required to remove the region dimension from land_mask.

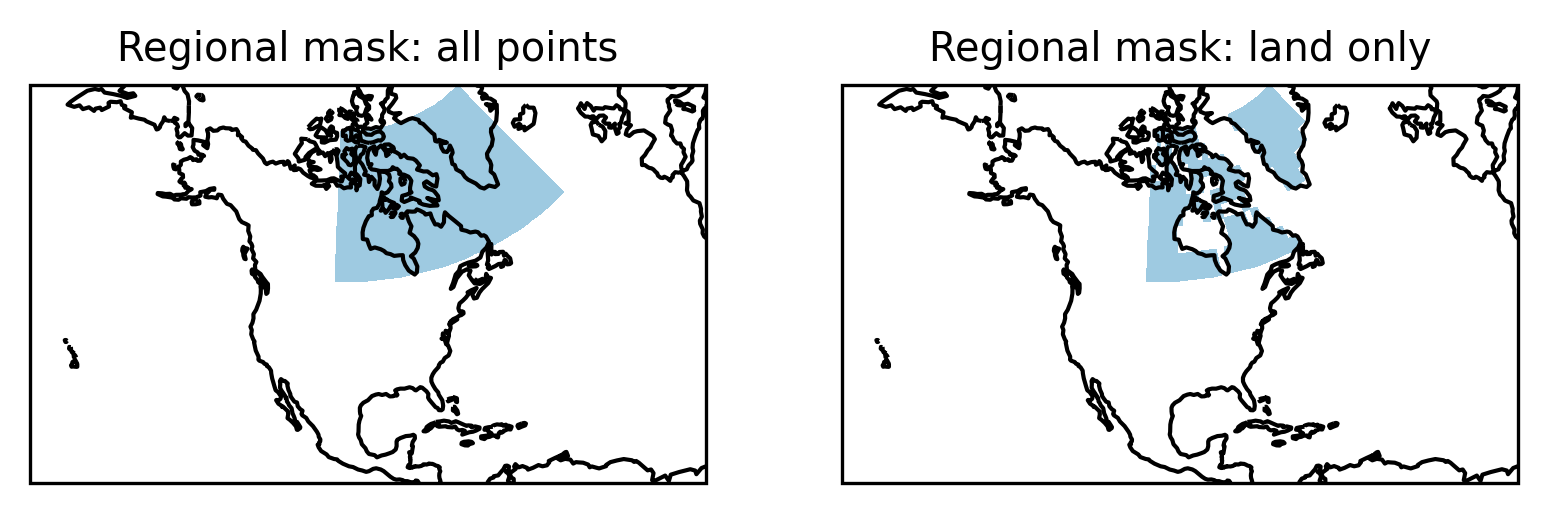
Finally, we compare the original mask with the one restricted to land points:

f, axes = plt.subplots(1, 2, subplot_kw=dict(projection=proj))

ax = axes[0]
mask_3D.sel(region=2).plot(
    ax=ax, transform=ccrs.PlateCarree(), add_colorbar=False, cmap=cmap1
)
ax.coastlines()
ax.set_title("Regional mask: all points")

ax = axes[1]
mask_lsm.sel(region=2).plot(
    ax=ax, transform=ccrs.PlateCarree(), add_colorbar=False, cmap=cmap1
)
ax.coastlines()
ax.set_title("Regional mask: land only");

References

• Special Report on Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation (SREX, Seneviratne et al., 2012)